Основные понятия

• Утверждение о равновероятности всех микросостояний носит название эргодической гипотезы. Она лжит в основе статистической физики.
• Вероятность макросостояния пропорциональна его статистическому весу.

  

Законы, принципы и соотношения

• S=klnΩ

  -формула Больцмана

• Ω=Ω₁*Ω₂

  -статистический вес макросостояния

Энтропия и вероятность

Если макросистема находится в неравновесном состоянии, то она самопроизвольно будет переходить в состояние с большей вероятностью —равновесное. Вместе с тем, согласно второму началу термодинамики все самопроизвольные процессы в замкнутых макросистемах сопровождаются возрастанием энтропии. Поэтому можно ожидать, что между энтропией S макросистемы в каждом состоянии и вероятностью Р того же состояния должна существовать определенная связь. Эта идея, высказанная Больцманом, оправдалась и оказалась весьма плодотворной.

Для нахождения этой связи рассмотрим обратимый процесс расширения идеального газа в пустоту. Пусть данный газ первоначально находится в объеме V₁ теплоизолированного сосуда объемом V₀. От остальной части сосуда он отделен перегород- кой (рис. *). 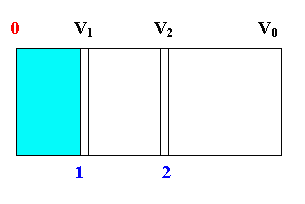Перегородку прак- тически мгновенно перемещают из положения 1 в 2, газ расширяется в пустоту до - объема V₂ и приходит в равновесное состояние.

В данном случае (газ идеальный) работу газ не совершает (А = 0), переданное газу тепло Q=0, следовательно, по первому началу приращение внутренней энергии ΔU = 0, т.е. температу- ра конечного и начального состояний одинакова.

Поскольку энтропия — функция состояния, то ее приращение в процессе V₁ —> V₂ можно вычислить по обратимому процессу, например, изотермическому.
В изотермическом процессе Q=A=עRTln(V₂/V₁) и ΔS=Q/T=עRln(V₂/V₁=kNln(V₂V₁), где N - число молекул в газе.

Теперь обратимся к вероятностям. В рассмотренном процессе распределение по скоростям в начальном и конечном состояниях одинаково: оно зависит только от температуры Т, которая не изменилась. Пространственное же распределение молекул стало более «свободным», а значит и более вероятным. В самом деле, вероятность нахождения одной молекулы газа в объеме V₁ равна, очевидно, V₁/V₀. Вероятность же всех N молекул собраться в объеме V₁ равна (V₁/V₀)^N. Обозначим эту вероятность как P₁. Соответственно (V₂/V₀)^N — как Р₂. Тогда отношение этих вероятностей

Р₂/Р₁=(V₂/V₁)^N

,
и приращение энтропии можно записать как

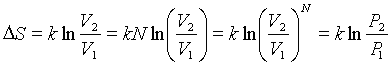
Поскольку вероятность макросистемы пропорциональна ее статистическому весу, т.е. Р ~Ω, последнюю формулу представим так:

ΔS=kln(Ω₂/Ω₁)

и мы приходим к знаменитой формуле Больцмана S=klnΩ, из которой и следует ΔS=kln(Ω₂/Ω₁)

Заметим, что приведенные здесь рассуждения не претендуют на вывод предыдущей формулы, а представляют собой скорее некоторые пояснения. Строгий вывод этой формулы дается в теоретической физике, где, кстати, показывается, что эта формула относится не только к равновесным состояниям, но и к неравновесным.

Теперь предположим, что макросистема состоит из двух практически не взаимодействующих подсистем, одна из которых находится в состоянии 1 с энтропией S₁ и статистическим весом Ω₁, а другая — в состоянии 2 с энтропией S₂ и статисти- ческим весом Ω₂.

Число способов (микросостояний), которыми может реализоваться рассматриваемое состояние макросистемы, равно произведению чисел способов, т.е. Ω₁ и Ω₂ которыми могут быть осуществлены состояния каждой из подсистем в отдельности:

Ω=Ω₁*Ω₂

Отсюда следует, что

S=kln(Ω₁*Ω₂)=klnΩ₁+klnΩ₂=>S₁+S₂,

как и должно быть, поскольку энтропия — величина аддитивная. Это, как видно, согласуется с формулой Больцмана.

Принцип возрастания энтропии со статистической точки зрения привел Больцмана к фундаментальному выводу: все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным.

При этом сама энтропия S характеризует степень беспоряд- ка в макросистеме: состояниям с большим беспорядком отвечает большая вероятность (или статистический вес Ω, чем у бо- лее упорядоченного состояния.